[논문 리뷰] EfficientNet 논문 리뷰 (Rethinking Model Scaling for Convolutional Neural Networks)

Transformer에 이어 ViT를 리뷰하려고 했으나,, 인턴 때 사용해보았던 Efficient Net이 급 궁금해져서 읽어보았습니다.

EfficientNet : Rethinking Model Scaling for Convolutional Neural Networks (2020)

논문 링크 : https://arxiv.org/abs/1905.11946

EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks

---

Abstract

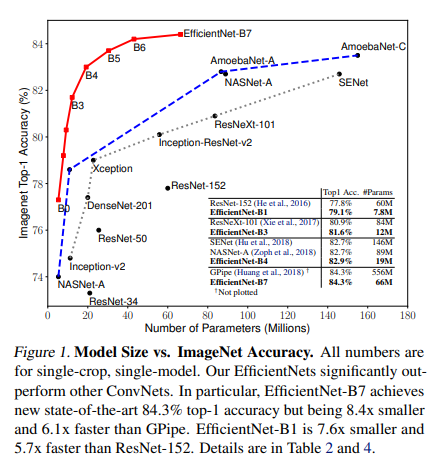
• CNN은 보통 fixed resource budget으로 개발된 후, resource가 더 충분해졌을 때 scaled up 되곤 함
• 이 연구에서는 model scaling에 대한 연구와, network depth, width, resolution 세 가지의 균형을 이루는 network가 더 나은 성능을 가진다는 것을 보임
• New scaling method를 제안 ( Compound Scaling Method )
  • depth/width/resolution 세 차원을 'compound coefficient'를 사용해 균일하게 scale하는 방법
• baseline network를 만들기 위해 neural architecture search를 사용함 -> scale up 해서 Efficient Net을 만듦
• 추론 시 기존 ConvNet보다 8.4x 더 작고 6.1x 더 빠른 성능으로 ImageNet SOTA 달성 (EfficientNet-B7)
• 훨씬 적은 parameter로 transfer 또한 잘 됨

---

Inroduction

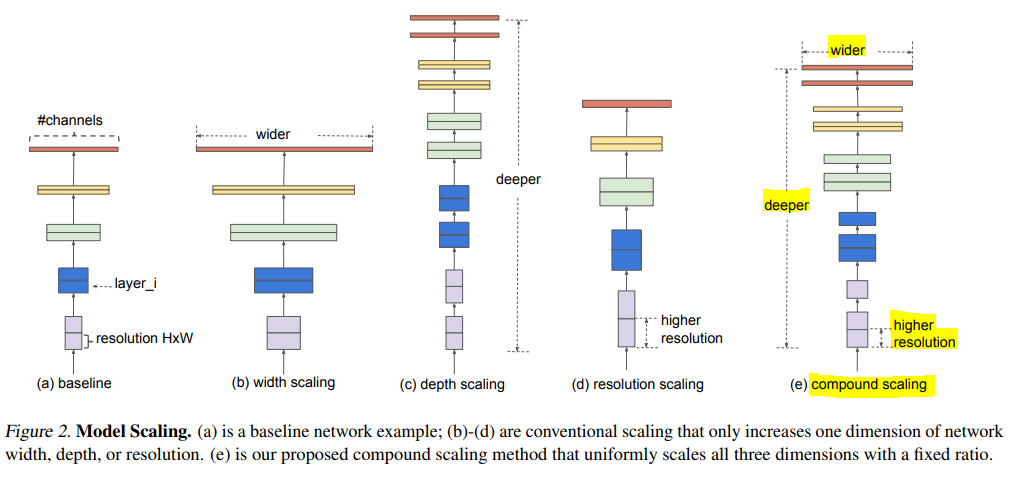
이전 연구에서는 depth, width, image size 중 하나만 scale하는 것을 주로 다룸

 

"더 나은 정확도와 효율성으로 ConvNet을 scale up 하는 정형적인 방법은 없을까?"

• 실증적인 연구에서 width, depth, resolution 세 가지의 균형을 잘 맞추는 게 중요함을 보임
• 상수 비율로 세 가지를 각각 scaling 하면 된다는 것을 알아냄

Compound Scaling Method를 제안

• 기존 연구에선 임의로 세가지 요소를 scale함
• 이 연구에선 network의 width, depth, resolution을 fixed scaling coefficient로 균일하게 scale함

오른쪽이 compound scaling

ex)

만약 $2^{N}$ 만큼의 computational resource를 더 사용할 수 있다면, 간단하게

depth를 $\alpha^{N}$ 로, width를 $\beta^{N}$로, image size를 $\gamma^{N}$ 로 증가시키면 됨 

(직관적으로 이미지가 크면, receptive field를 늘리기 위해 더 많은 layer가 필요하고, 더 미세한 pattern을 얻기 위해 더 많은 channel이 필요하기 때문)

 

 

model scaling 의 효과는 baseline network에 따라 다름

• baseline network를 만들기 위해 neural architecture search를 사용했고, model의 조합을 scale up 해서 EfficientNet을 만듦

널리 사용되는 ResNet-50 과 비교했을 때도 비슷한 FLOP으로 EfficientNet-B7이 accuracy가 높았음

EfficientNet은 transfer도 잘 되고, 8개중 5개의 dataset에서 훨씬 적은 parameter로 SOTA accuracy를 달성함

---

Related Work

(1) ConvNet Accuracy

기존 ConvNet SOTA 연구들은 너무 크고, ImageNet을 위해 만든 모델들임

요즘 연구들은 다양한 전이 학습 데이터셋에서도 잘 동작하는 것을 보임

-> 하지만 hardware memory limit이 있기 때문에 더 나은 효율성이 필요함

 

(2) ConvNet Efficiency

Model compression은 효율성을 위해 accuracy를 희생해 model size를 줄이는 방법

SqueezeNets, MobileNets, ShuffleNets 등 효율적인 mobile-size의 ConvNet도 등장함

 

-> 이 연구에서는 아주 큰 ConvNet을 위한 모델을 효율적으로 학습하는 게 목표

 

(3) Model Scaling

ConvNet을 scale하는 다양한 방법이 있음

• ResNet의 경우 network depth(#layers)를 조절
• MobileNet의 경우 network width(#channels)를 조절
• image size 조절

->depth와 width가 둘 다 ConvNet에서 중요하다는 연구는 있었지만, ConvNet을 어떻게 효율적으로 scale 할 것인지는 아직 남아있는 문제였음

---

Compound Model Scaling

(1) Problem Formulation

$Y_{i} = F_{i}(X_{i})$

$X_{i}$ : input tensor

$X_{i}$ shape : $<H_{i}, W_{i}, C_{i}>$

• $H_{i},W_{i}$ : spatial dimension
• $C_{i}$ : channel dimension 

$\mathcal{N} = F_{k} \odot ... \odot F_{2} \odot F_{1}(X_{1}) = \odot _{j=1,...,k} F_{j}(X_{1})$

ConvNet은 보통 multiple stage로 분할되고 각 stage의 모든 layer들은 같은 구조임

따라서 ConvNet은 

$\mathcal{N} = \odot_{i=1...s} F_{i}^{L_{i}}(X_{<H_{i}, W_{i},C_{i}>})$ 로 표현할 수 있음

 

representative ConvNet

Spatial dimension은 줄어들고, channel dimension은 늘어나는 것을 알 수 있음

ex) <224,224,3> -> <7,7,512>

 

ConvNet은 best architecture $F_{i}$ 를 찾는 데 중점

Model Scaling은 미리 정의된 baseline $F_{i}$은 건들지 않고, width($C_{i}$), length($L_{i}$), Resolution($H_{i}, W_{i}$)을 확장하는 데 중점을 둠

• 모든 layer는 상수 비율로 균일하게 scale 되어야 함

주어진 제약 조건에서 model accuracy를 최대화하는 게 목표

-> optimization problem으로 정의될 수 있음

optimization problem

(2) Scaling Dimensions

위 optimization problem은 해당 제약조건 아래 ,d,w,r 이 dependent하기 때문에 풀기 어려움

-> 그동안 이로 인해 세 차원 중, 하나로만 scale 하는 방법이 많음

 

width, depth, resolution 각각의 accuracy gain

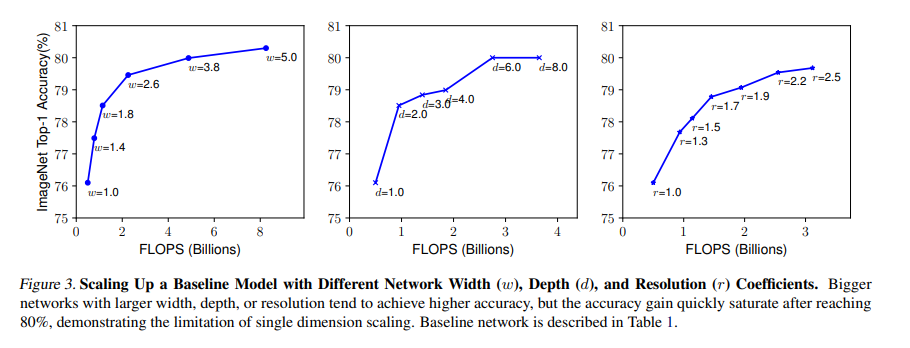
<Observation 1>
width, depth, resolution 중 어느 dimension을 scale up 해도 아주 큰 model에서는 accuracy gain이 감소함

 

Depth(d)

• ConvNet은 깊이가 깊을수록, 더 풍부하고 복잡한 feature를 학습하고, 다른 문제에도 일반화가 잘 됨
• 하지만 vanishing gradient 문제로 학습시키기가 어려움
  • skip connection, batch normalization 등의 해결 방법이 있지만, 아주 깊은 경우에 효과가 없음
  • ex ) ResNet-1000, ResNet-101의 경우 비슷한 accuracy를 보임

Width(w)

• 작은 size의 모델에서 주로 쓰임
• wider network는 fine-grained feature를 뽑아낼 수 있고 학습시키기 더 쉬움
• 그러나 아주 넓고 얕은 network의 경우 higher level feature를 뽑아내기가 힘듦

 

Resolution(r)

• 높은 resolution의 이미지의 경우 fine-grained feature를 뽑아내기 쉬움
• 마찬가지로 너무 높은 resolution 의 경우 accuracy gain이 더뎌지는 걸 확인할 수 있음

 

(3) Compound Scaling

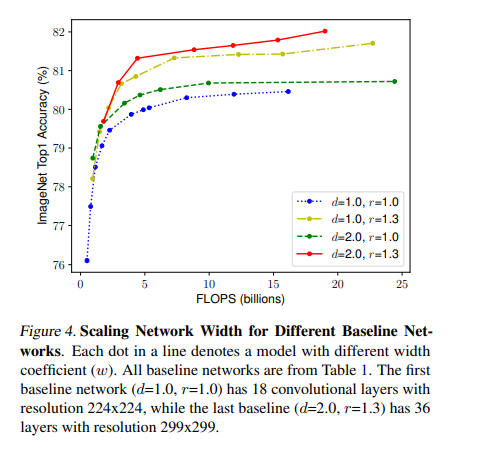
<Observation 2>
Scaling 시, 더 나은 정확도와 효율을 위해서는 width, depth, resolution 간 균형을 잘 맞추는 것이 중요함

 

 

Compound Scaling Method

compound coefficient $\phi$로 width, depth, resolution을 균일하게 scale하는 방법

depth : $d= \alpha^{\phi}$

width : $w= \beta^{\phi}$

resolution : $r= \gamma^{\phi}$

s.t. $\alpha \cdot \beta^{2} \cdot \gamma^{2} \approx 2$

      $\alpha \geq 1, \beta \geq 1, \gamma \geq 1$

 

$\phi$ 는 user-specified coefficient로, user의 사용가능한 resource에 맞게 지정하면 됨

$\alpha, \beta, \gamma$는 width, depth, resolution 각각의 extra resource를 의미함

 

일반적인 convolution 연산에서 FLOP은 $d,w^{2},r^{2}$ 의 비율로 계산됨

ex) depth를 두 배로하면, FLOP도 두 배가 되지만, width나 resolution을 두 배로 하면, FLOP은 네 배가 됨

-> FLOP은 $(\alpha \cdot \beta^{2} \cdot \gamma^{2})^{\phi}$ 로 계산될 수 있음

이 연구에서는 $\alpha \cdot \beta^{2} \cdot \gamma^{2} \approx 2$ 라는 조건으로, FLOP이 약 $2^{\phi}$ 로 증가함

---

EfficientNet Architecture

Model Scaling은 baseline network의 layer operation $F_{i}$를 바꾸지 않는다고 했었음

-> 따라서, 처음부터 좋은 baseline network를 정하는 것이 중요함

-> mobile-size의 baseline을 개발함 (= EfficientNet )

EfficientNet Baseline 구조

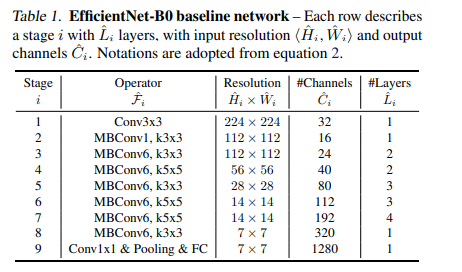
$\alpha, \beta, \gamma$를 찾아 큰 모델에 적용하면 더 좋은 성능을 내는 것이 가능했지만,

큰 모델의 경우 이 값을 찾는 비용이 더 많이 들었음

 

이 연구에서는 다음 두 단계를 이용해 이 문제를 해결함

[step1]

$\phi = 1$로 고정한 뒤, resource가 두 배로 있다고 가정하고 eqn 2,3 을 이용해 $\alpha, \beta, \gamma$를 찾음

[step2]

이번엔 $\alpha, \beta, \gamma$ 를 고정하고 $\phi$ 값을 바꿔서 baseline network를 scale up 함

 

$\phi$ 값만을 수정해 B0~B7까지 만듦

---

Experiments

기존 ConvNet들에서, 새로 제안한 EfficientNet에서의 scaling method 실험을 각각 다룸

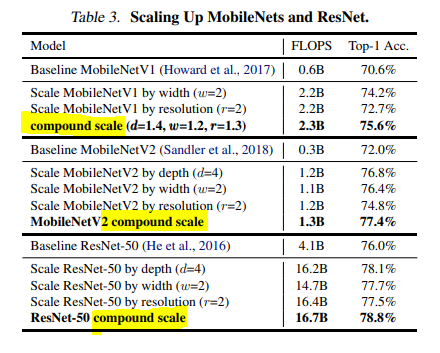
(1) Scaling up MobileNets and ResNets

MobileNet, ResNet에 모두 적용해 보았을 때,

single-dimension에 대한 scaling method보다 compound scaling method가 성능이 더 좋은 것을 확인할 수 있음

single/compound 비교

(2) ImageNet Results for EfficientNet

더 적은 parameter와 FLOP으로도 더 좋은 성능을 보임

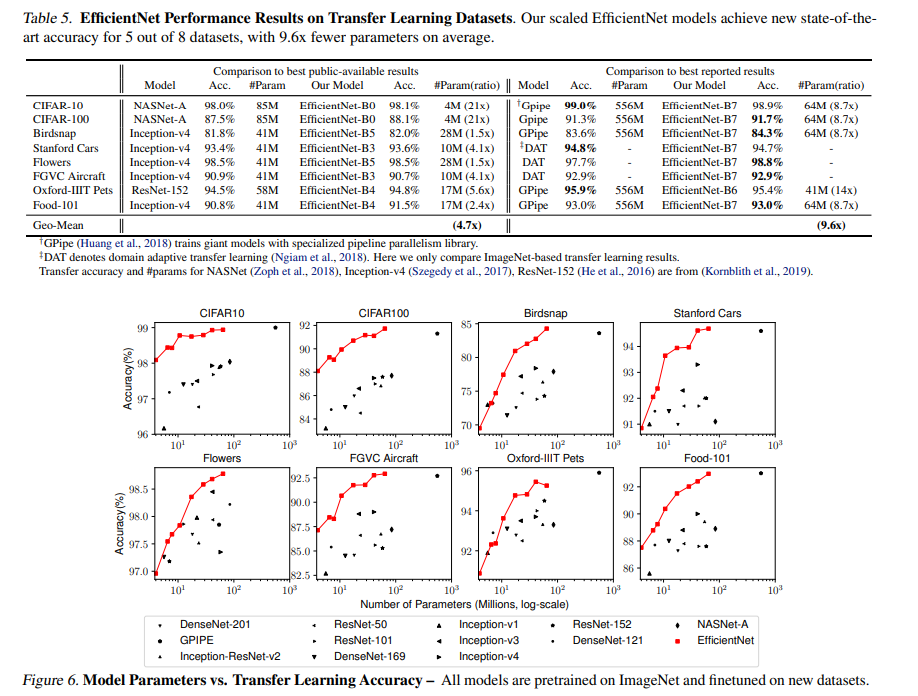
(3) Transfer Learning Results for EfficientNet

전이 학습에서도 좋은 성능을 보임

---

Discussion

acivation map

compound scaling을 적용한 모델이 object detail과 relevant region을 더 잘 캐치하는 경향이 있음

---

Conclusion

• width, depth, resolution 간 균형이 model을 scale up 하는 데 중요한 요소였음을 보임
• accuracy가 더 높고 효율적이면서, 쉽게 모델을 scale up 할 수 있는 방법을 제안함 
• 전이 학습에서도 더 적은 parameter와 FLOP으로 잘 동작함을 보임

---

인턴 생활을 하며 다녔던 회사에서 efficient net을 자주 사용했었는데, 이제 efficient net이 왜 그렇게 자주 사용되었는지 알 것 같습니다. 이름이랑 어울리는 network라는 생각이 들었습니다 ㅎㅎ

요즘 수식을 작성하는 데 LaTeX를 자주 사용하다보니, 블로그에서 LaTeX를 사용하는 방법이랑 자주 쓰이는 것들을 정리해보면 좋을 것 같더라구요. 시간이 되면 한번 정리해보려합니다!